O primeiro passo foi entender o algorimo. Em sala nos foi mostrado que o algoritmo de Bresenham é utilizado para imprimir pixels em uma linha reta calculando o próximo pixel a ser preenchido com base em um ponto médio entre dois pixels verticais e no coeficiente angular da reta. Porém, o algoritmo só funcionava para o primeiro octante, ou seja, para ângulos menores ou iguais a 45°. A grande vantagem do algoritmo de Bresenham é a sua eficiência, pois não realiza séries de operações de divisão e arredondamento.
Algoritmo de Bresenham:
Nota: As imagens foram retiradas do blog Learning Bits, porém, as imagens contendo as fórmulas são originais do Wikipedia-EN (Bresenham line algorithm).
Baseada na explicação do algoritmo por Learning Bits, temos:
Dados dois pontos, considere que o ponto (x1,y1) seria o inferior esquerdo, e (x2,y2) o superior direito. Assim, veja a imagem abaixo:
1 - Tomada de decisão por algoritmo do ponto médio (algoritmo de Bresenham)
Seguindo a imagem, o último ponto pintado foi o ponto P e o próximo pode ser o ponto I ou o ponto S. O algoritmo de Bresenham utiliza um ponto médio M entre os dois pontos possíveis e um ponto Q da reta com a mesma coordenada x que M. Logo, se M está acima de Q, o ponto a ser pintado é o de baixo e, caso contrário, o de cima. Por esse motivo, esse algoritmo também é chamado de algoritmo do ponto médio.
O método para calcular se o ponto M está acima ou abaixo da reta é:
O método para calcular se o ponto M está acima ou abaixo da reta é:
dX = x2-x1 & dY = y2-y1
Sendo a equação da reta:
Definimos então a função:
Multiplicando os valores da equação por dX:
O modelo da equação acima é:
Sendo assim, f(x, y) = 0 para pontos na reta, f(x, y) < 0 para pontos abaixo da reta e f(x, y) > 0 para pontos acima da reta. Então, usaremos d como uma variável de decisão e, usando as coordenadas do ponto M da imagem, temos:
Se d > 0, o ponto S deverá ser pintado, se d < 0 o ponto I deverá ser pintado e, se d = 0, qualquer um dos pontos pode ser pintado sem influenciar na visualização da reta.
Logo:
Caso o ponto I tenha sido escolhido:
Caso o ponto S tenha sido escolhido:
Porém, esse algoritmo só funciona para o primeiro octante e para o seu oposto, contanto se que invertam os pontos inicial e final da reta antes de realizar as operações. Para adequar aos outros octantes, devemos alterar os valores de d, como mostrado na tabela:
2 - Variação do algoritmo para todos os octantes
A primeira coluna da tabela mostra as relações do coeficiente angular da reta (m) que é usado para definir o octante em que se encontra a reta. A segunda mostra o valor inicial de d, tratado no texto acima também como dold. A terceira e a quarta colunas mostram o caso em que d é maior ou igual a 0: quais coordenadas devem ser incrementadas no ponto m e o quanto aumenta o valor de d. A quinta e a sexta colunas mostram o mesmo que a terceira e a quarta, mas para os valores em que d é menor do que 0.
São 4 possíveis operações para os valores de d, pois a operação utilizada para um octante, serve para o seu oposto contanto que se invertam os pontos iniciais e finais da reta.
3 - Teste do algoritmo desenhando linhas nos octantes
Descrição do código:
Foram criados os structs cor e ponto. Cor continha os valores de RGBA e Ponto continha as coordenadas x e y do ponto escolhido. Cor e coordenadas não foram colocadas no mesmo struct para tornar mais fácil a leitura e compreensão do código. Em seguida foi implementada a função putPixel que exibia um ponto na tela escrevendo na memória de vídeo. Foram criadas, também, 5 funções drawLine: uma para cada octante e seu oposto e uma para retas verticais, com as quais tive problemas em lidar nas funções dos octantes 2, 3, 6 e 7. Em seguida, foi criada uma função com o nome drawLine que verificava o valor do coeficiente angular da reta (m) com base nos pontos inicial e final da mesma e a posição dos pontos, então os passava para a função drawLine correspondente ao octante com os pontos na ordem correta. Cada função drawLine verificava o valor de d, selecionava o ponto a ser pintado, incrementava os valores do ponto M e usava a função putPixel em um laço de repetição while para pintar sequencialmente todos os pontos da reta.
4 - Teste da função drawTriangle (há um pixel de cor diferente no ponto inferior esquerdo e no ponto superior devido à um bug que só ocorre quando o ponto inicial é verde (componente RGB: 0, 255, 0).
Com relação à variação das cores. Foram selecionadas as cores dos pontos iniciais e finais, então basta que cada um dos componentes RGB seja calculado da seguinte forma:
cor.r = (cor1.r - cor2.r)/l
l = pontof.x - pontoi.x(para retas horizontais ou inclinadas)
l = pontof.y - pontoi.y(para retas verticais ou inclinadas)
l é a distância entre os pontos inicial e final da reta, porém, usar a equação da hipotenusa para retas diagonais estava causando um erro que fazia com que a escala terminasse no ponto médio da reta e se repetisse até o final da mesma.
As cores e os pontos foram passados como parâmetros.
Referências:
Imagens das fórmulas utilizadas no cálculo retiradas de:
https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm
Imagens 1 e 2 retiradas de e explicação do algoritmo baseada em:
http://letslearnbits.blogspot.com.br/2014/10/icgt1-algoritmo-de-bresenham.html
Imagens 3 e 4 originais de teste do programa produzido.
Outras referências:
https://www.cs.helsinki.fi/group/goa/mallinnus/lines/bresenh.html
https://jansebp.wordpress.com/2012/12/16/icg-t1-rasterizacao/
Foley, J. D.; van Dam, A.; Fundamentals of Interactive Computer Graphics. Addison Wesley. 1982.
Foley, J. D.; van Dam, A.; Feiner, S. K.; Hughes, J. F. Computer Graphics: Principles and Practice. 2a edição. Addison-Wesley Professional, 1996.
Slides de aula da disciplina Introdução à Computação Gráfica (Rasterization), Professor Christian Azambuja Pagot CI/UFPB (Currículo lattes).
Nota: o código foi feito em C.
Nota menos útil: o teste com a função drawTriangle me lembrou






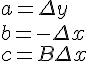







Nenhum comentário:
Postar um comentário